Data Layout Semantic Conversion

This document, which is originally written in the introducing blog, covers the layout semantic divergence between TensorFlow Lite (TFLite) models which is NHWC and ONNX which is NCHW.

The data layout format of TFLite has not been mentioned in either the document or the model representation but in the implicit agreement of the TFLite converter (the TensorFlow model needs to be NHWC) and the kernels. On the contrary, ONNX explicitly declares that it uses NCHW in both operator representation and document (which is generated from operator representation).

tflite2onnx introduces propagation based approach to handle the layout issue in general, together with some other mechanisms for dedicated corner cases.

Propagation based Approach

The propagation based approach is introduced to resolve this by propagating the layout semantic divergence across the graph, in which way the transpose pattern is not needed.

By default (for most cases), given a graph, some of the tensors have implicit layout semantic, e.g. tensors that are connected to Conv directly, while others are not, e.g. Abs and Add. The later ones are transparent to layout, where transparent means all of the tensors that connected to the operator mush have the same layout semantic or don’t hold such semantic.

So when an operator that is transparent to layout is connected to an operator that has implicit layout tensors, then all tensors of the transparent operator have the same layout semantic as the tensor that connecting these two operators, named as propagation.

For example, when converting the TFLite graph (omitted kernel and bias) \(\left< A_{nhwc} \right> \rightarrow [Conv] \rightarrow \left< B_{nhwc} \right> \rightarrow [Abs] \rightarrow \left< C_{?} \right>\) to ONNX, tensor \(\left< A_{nhwc} \right>\) becomes \(\left< A_{nchw} \right>\) and \(\left< B_{nhwc} \right>\) becomes \(\left< B_{nchw} \right>\). Hence, the output \(\left< C \right>\) of \([Abs]\) should have the same format as the input \(\left\). Propagation based approach propagates the conversion from \(\left\) to \(\left< C \right>\). Therefore we have the ONNX graph \(\left< A_{nchw} \right> \rightarrow [Conv] \rightarrow \left< B_{nchw} \right> \rightarrow [Abs] \rightarrow \left< C_{nchw} \right>\), where no additional operators nor tensors are introduced.

During layout propagation, the layout transformation permutes the shape of tensors if they are activations, i.e. value info in ONNX, and transposes the data of weights in addition, i.e. initializer in ONNX.

In practice, operators are categorized into four (as marked in Figure 5):

Implicit: operators have layout semantic divergence, e.g. Conv. They are the source of layout semantic divergence.
Transparent: operators that are insensitive to layout, e.g. Abs. If any tensor has layout semantic divergence, propagate it to all tensors that are connected to such operators.
Attribute: operators that can propagate layout semantic divergence just like Transparent, but have layout sensitive attributes that need special handling, e.g. attribute axis of Concat. An additional pass after propagation to adjust these attributes is required.
Terminate: operators that don’t have and cannot propagate layout semantic divergence, e.g. Reshape. The propagation across the graph terminates at such operators.

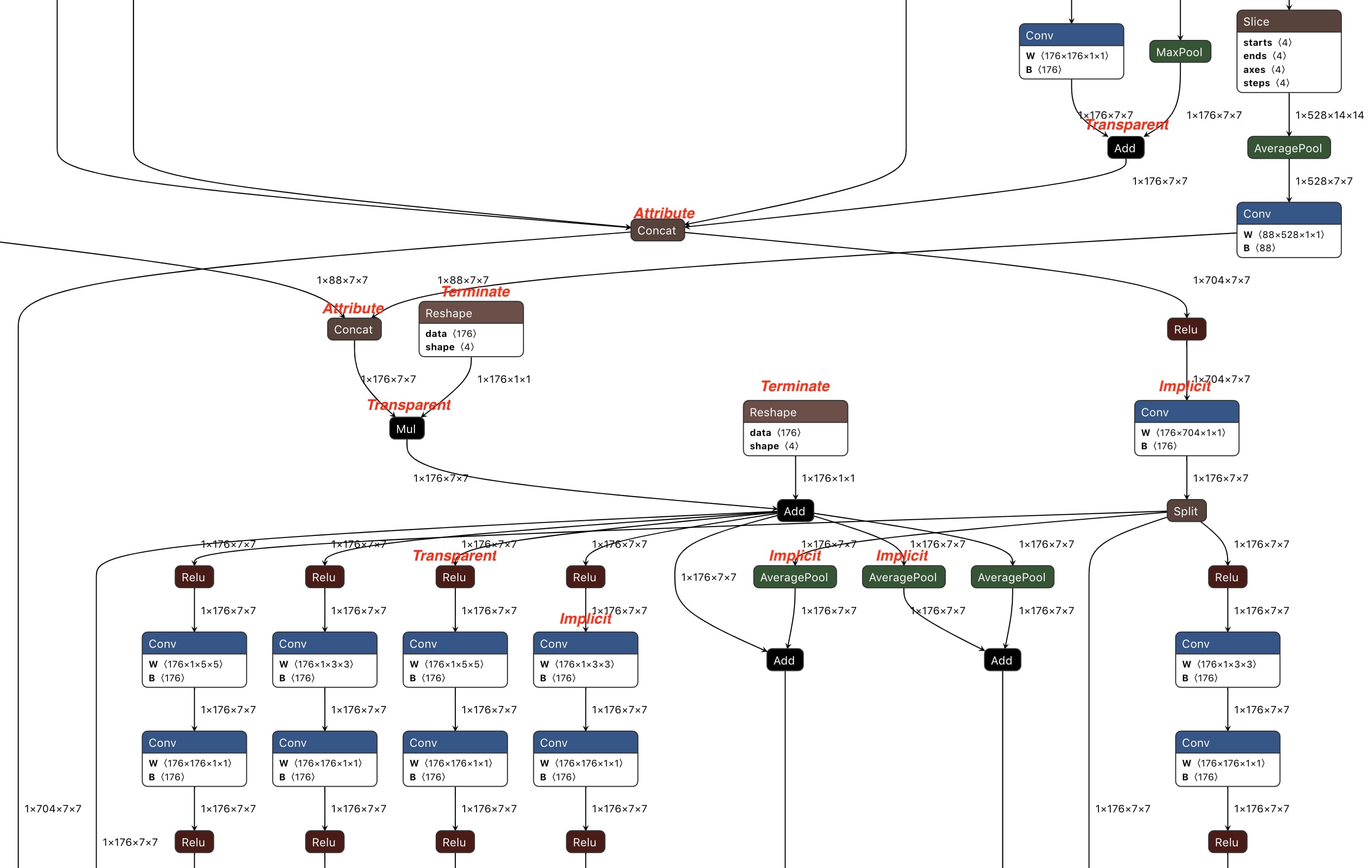Part the ONNX model generated by *propagation based approach*. Figure 1: Part of the ONNX model generated by propagation based approach of TFLite2ONNX

When propagating layout semantic divergence across the graph, for a particular operator: if it is Transparent or Attribute, propagate layout semantic divergence among its tensors; if it is Implicit or Terminate, terminates the propagation in this direction. Figure 1 is part of the ONNX model generated by propagation based approach from the NASNet TFLite model.

Explicit Layout

With propagation based approach, the converted ONNX model includes zero effort to handle layout semantic divergence, i.e. no additional operators or tensors are introduced.

However, sometimes there could be incompatible layouts. Consider Reshape, which is Terminate, as below. If \(\left< A \right>\) is propagated while other tensors are not, the output layout could be unexpected as the user may assume the dimensions of \(\left\) has something to do with \(\left< A \right>\). (Transpose based approach doesn’t have this issue as its layout is TFLite style at the model level, layout semantic divergence is handled inside the \([Transpose] \rightarrow [OP] \rightarrow [Transpose]\) pattern.)

\[\left. \begin{aligned} \{Graph\} \rightarrow \left< A \right> \rightarrow [Reshape] \rightarrow \left \\ \left< C \right> \\ \end{aligned} \right\} \rightarrow [Concat] \rightarrow \left< D \right>\]

Explicit layout is introduced to handle such a scenario. Users can feed a mapping of \(\{Tensor\ name : tuple(TFLite\ layout, ONNX\ layout)\}\) that describes the data layout of TFLite and ONNX to TFLite2ONNX. And, it’s flexible for the user to define the layout conversion for non-_Transparent_ operators. For example, we have performed the NHWC to NCHW layout conversion for a TFLite graph that has only an Add operator.

Broadcast of Propagation

Another problem is the broadcast of binary operators such as Add (see this issue for more). Taking the example below, in which tensor \(\left\) needs to be broadcasted. If \(\left< A \right>\) is converted from NHWC to NCHW, i.e. \(\left< A_{(2 \times 5 \times 3 \times 4)} \right>\), \(\left\) is no longer broadcastable in ONNX. Even worse, the layout semantic divergence will fail when propagated to \(\left\) as \(\left< A \right>\) and \(\left\) have different dimensions.

\[\left. \begin{aligned} \{Graph\} \rightarrow \left< A_{(2 \times 3\times 4 \times5)} \right> \\ \left< B_{(4 \times 5)} \right> \\ \end{aligned} \right\} \rightarrow [Add] \rightarrow \left< C \right>\]

To manage broadcasting in the ONNX model, tflite2onnx introduces the Reshape pattern. Any tensors like \(\left\) are reshaped to extend (inserting \(1\)) their dimensions to be equal with the other, such that propagation and broadcasting can correctly do their jobs. The example of the intermediate graph before propagation is as below.

\[\left. \begin{aligned} \{Graph\} \rightarrow \left< A_{(2 \times 3\times 4 \times5)} \right> \\ \left< B_{(4 \times 5)} \right> \rightarrow [Reshape] \rightarrow \left< B^{'}_{(1 \times 1 \times 4 \times 5)} \right>\\ \end{aligned} \right\} \rightarrow [Add] \rightarrow \left< C \right>\]